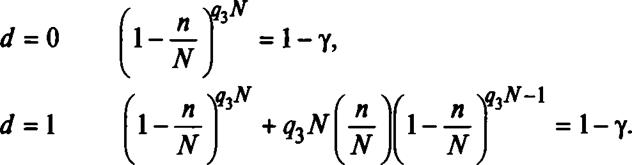Подтверждение требований к вероятности безотказной работы партии изделий

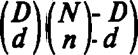При выборочном контроле партии продукции задается допустимое число отказов d3 или уровень дефектности q3 = D/N, равный 1 — В этом случае используется гипергеометрическое распределение

где N— объем партии; D — число дефектных изделий в партии; п — объем выборки; d — наблюдаемое в выборке число отказов:

N ,

Ui d(D-d)V «/ n(N-п)’

(N — D ___________ (N-D)__________

n-dj (n-d)[(N-n)-(D-d)]’.’

При N -»оо гипергеометрическое распределение стремится к биномиальному. Оценка вероятности выполнения задачи в этом случае совпадает с оценкой параметра биномиального распределе­ния R = -d/n = m/n, однако имеет меньшую дисперсию: /)[/?] = R(l-R)N-n

= — ——— —-. Решающим правилом при проверке гипотезы Я — Q3

(соответственно R < R3) при альтернативной гипотезе д < д3 (или

R> R3) является дъ > д3, где верхняя доверительная граница дъ = DB/N определяется из соотношения

P{r<d}=YP(r/n, N,DB) = 1-у.

г=О

Так как таблицы интегральной функции гипергеометрического распределения имеются лишь в узкоспециальных изданиях, для прак­тических расчетов используется биномиальная аппроксимация. При d = 0 и d = 1 имеем следующие простые формулы, позволяющие рассчитать критический объем выборки:

В табл. 13.10 и 13.11 приведен критический объем выборки при различной доверительной вероятности у, числе дефектных изделий D и числе отказов d = 0 и d Прочерки в таблицах означают, что объема партии не хватает для принятия решения. В правой графе каждой таблицы приведен объем выборки при использовании бино­миального распределения, рассчитанный по формулам:

d = 0 (1-?з)" = 1-у,

d = l (1-^з)"+л(1-^з)л_1^з = 1-у.

Как следует из сравнения данных таблиц, учет объема партии, особенно для мелкосерийного производства, приводит к существен­ному снижению необходимого объема испытаний.

Значение вероятности J?2, необходимое
для реализации числа испытаний из табл. 13.9 (d = 0)